ResNet的提出是为了解决梯度消失问题吗？
残差思想是什么？
本文简单回顾一下ResNet，重点理解其中的残差学习思想。
首先推荐一个链接：
知乎专栏-机器学习算法工程师
本文参考：
Deep Residual Learning for Image Recognition
Identity Mappings in Deep Residual Networks
Gradient Vanish
在接触神经网络的时候，我们都学习过梯度消失这个概念。梯度消失的根源在于深度神经网络和反向传播。目前深度学习方法中，GPU加速运算以及深度神经网络的发展使得我们可以构建更深的网络完成更复杂的任务。
但是目前优化神经网络的方法都是基于反向传播思想的，即：根据损失函数计算的误差通过梯度反向传播的方式，指导深度网络权值的更新优化。这样做是一定原因的，我们在模拟GD、SGD一文中了解过其更新方式。首先深层网络由许多非线性层堆叠而成，每一层非线性层都可以看作是一个非线性函数 $f_i(x)$（非线性来自非线性激活函数），因此整个深度网络可以视为是一个复杂的非线性多元函数：
$$ F(x) = f_n(…f_3(f_2(f_1(x)*\theta_1 + b) * \theta_2 +b)) $$
我们最终的目的是希望这个多元函数可以很好的完成输入到输出之间的映射，假设不同的输入，输出的最优解是 $g(x)$ ，那么，优化深度网络就是为了寻找到合适的权值，满足 $Loss = L(g(x), F(x))$ 取得极小值点，比如最简单的MSE Loss。
随着深度的加深，激活函数的作用，根据链式法则，传到浅层的梯度越来越小，直至无法感应，或者即使感应也推不动进一步的学习。这就是所谓的梯度消失问题。
Degradation Problem
但是ResNet的提出并不是为了解决梯度消失问题，因为当时梯度消失已有BN等方式可以缓解了。 从经验来看，网络的深度对模型的性能至关重要，当增加网络层数后，网络可以进行更加复杂的特征模式的提取，所以当模型更深时理论上可以取得更好的结果，或许之前我们还会讨论更深的网络其性能一定会更好吗？
首先讲网络的退化问题与过拟合问题区分开来，这个现象可以在下图中直观看出来：56层的网络比20层网络效果还要差。观察到56层网络的训练误差同样高，所以这不会是过拟合问题。
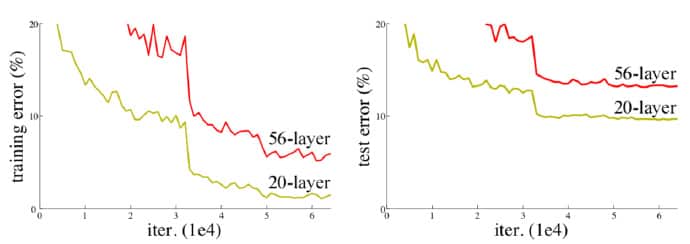
实验发现深度网络出现了退化问题（Degradation problem）：网络深度增加时，网络准确度出现饱和，甚至出现下降。
我们知道深层网络存在着梯度消失或者爆炸的问题，这使得深度学习模型很难训练。但是现在已经存在一些技术手段如BatchNorm来缓解这个问题。但也只是缓解，并不能完全或者说更进一步解决这个问题。
Residual Learning
训练精度的退化表明了不是所有的系统都同样好优化，好训练的。为了解决一个复杂问题，我们先考虑简单的情况。
现在你有一个浅层网络，你想通过向上堆积新层来建立深层网络，一个极端情况是这些增加的层什么也不学习，仅仅复制浅层网络的特征，即这样新层是恒等映射（Identity mapping）。在这种情况下，深层网络应该至少和浅层网络性能一样，也不应该出现退化现象。好吧，你不得不承认肯定是目前的训练方法有问题，才使得深层网络很难去找到一个好的参数。
这个有趣的假设让何博士灵感爆发，他提出了残差学习来解决退化问题。
对于一个堆积层结构（几层堆积而成）当输入为 $x$ 时，其学习到的特征记为$H(x)$，这是一个直接从输入 $x$ 到输出的映射，使其可以被这几层堆积结构所拟合。假设多个非线性层可以逐渐逼近复杂函数，则相当于它们可以逐渐逼近残差函数。所以，与其希望直接拟合到 $H(x)$，不如现在我们希望其可以学习到残差 $F(x) = H(x) - x$，这样其实原始的学习特征是 $H(x) = F(x) + x$。
虽然两种形式都应该能够逐渐逼近所需的函数，但学习的难易程度可能会有所不同1 。当残差为0时，此时堆积层仅仅做了恒等映射，至少网络性能不会下降，实际上残差不会为0，这也会使得堆积层在输入特征基础上学习到新的特征，从而拥有更好的性能。残差学习的结构如图4所示。这有点类似与电路中的“短路”，所以是一种短路连接（shortcut connection）。
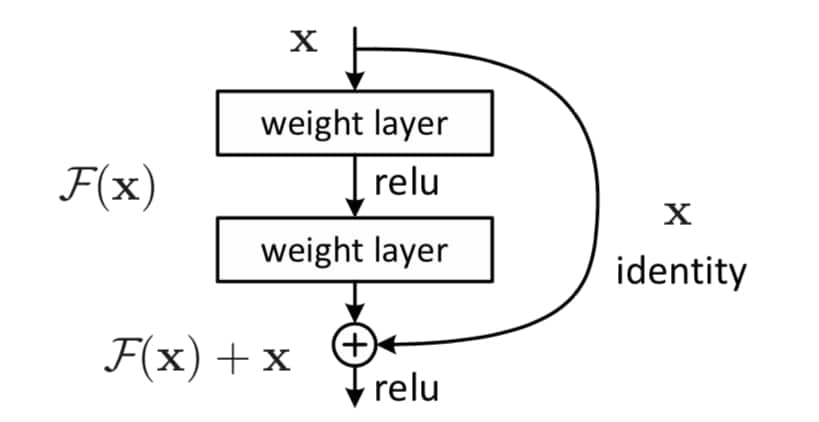
为什么残差学习相对更容易，从直观上看残差学习需要学习的内容少，因为残差一般会比较小，学习难度小点。在Identity Mappings in Deep Residual Networks 中，何博士从数学的角度来分析这个问题，首先残差单元可以表示为：
$$ y_l = h(X_l) + F(X_l, W_l), X_{l+1} = f(y_l)$$
其中$X_l, X_{l+1}$ 分别表示第$l$层残差单元的输入和输出，注意每个残差单元一般包含多层结构。$F$是残差函数，表示学习到的残差，而$h(X_l) = X_l$表示恒等映射，$f$是ReLU激活函数。基于上式，我们求得从浅层$l$到深层$L$的学习特征为：
$$ X_L = X_l + \sum\limits_{i=l}^{L-1}F(X_i, W_i) $$
利用链式法则，可以求得反向过程的梯度：
$$ \frac{\partial loss}{\partial {X_l}} = \frac{\partial loss}{\partial {X_L}} \cdot \frac{\partial {X_L}}{\partial {X_l}} = \frac{\partial loss}{\partial {X_L}} \cdot \lgroup 1 + \frac{\partial}{\partial {X_L}} \sum\limits_{i=l}^{L-1} F(X_i, W_i) \rgroup $$
小括号中的1表明短路机制可以无损地传播梯度，而另外一项残差梯度则需要进过带有weights的层，梯度不是直接传递过来的。残差梯度不会那么巧全为-1，而且就是比较小，有1的存在也不会导致梯度消失。所以残差学习会更容易，所以残差网络可以很大程度上缓解梯度消失问题。
Network Architectures
ResNet网络结构是参考了VGG19网络，在其基础上进行了修改，并通过短路机制加入了残差单元，如下图所示。主要的变化体现在ResNet直接使用stride=2的卷积做下采样，并且最后使用global average pooling代替了全连接层。
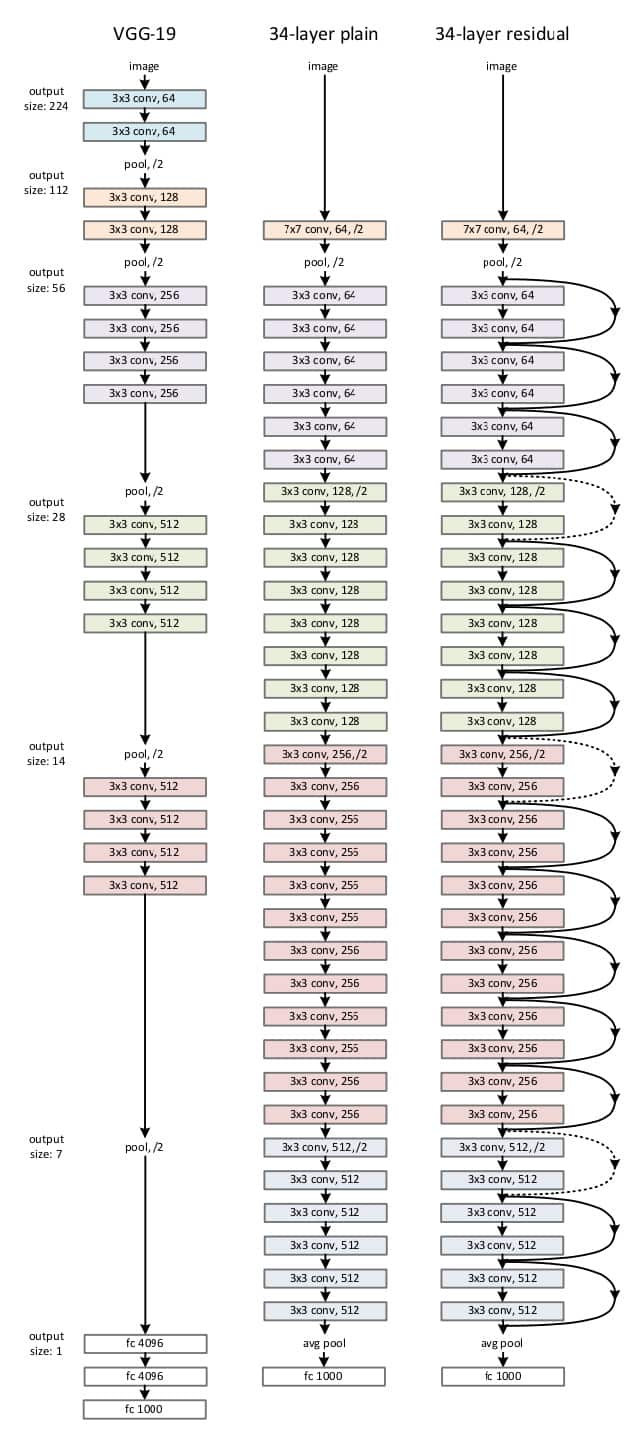ResNet的一个重要的设计原则是：当feature map大小降低一半时，feature map的数量增加一倍，这就保持了网络层的复杂度。从上图可以看出，ResNet相比普通网络每两层之间增加了短路机制，这就形成了残差学习。其中虚线表示feature map数量发生了变化。
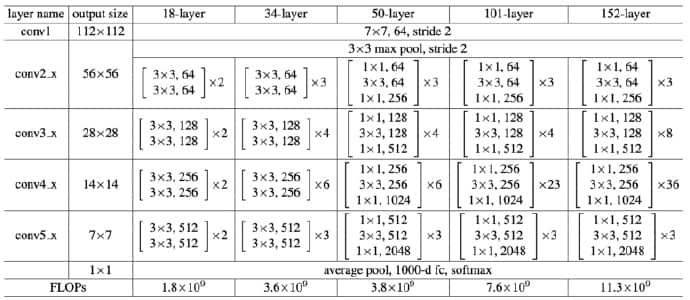
我们可以根据上表构建更深的网络。对于18-layer和34-layer的ResNet，其进行的是两层间的残差学习，当网络更深时，其进行的是三层间的残差学习。三层卷积核分别是1x1,3x3,1x1。
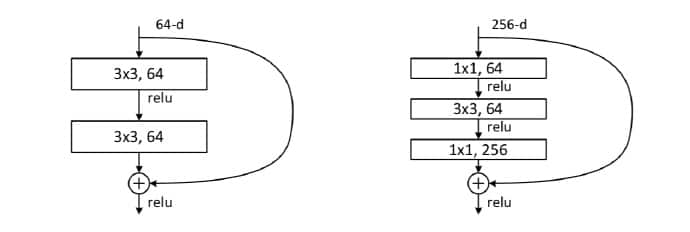
上图为ResNet使用的两种残差单元。对于短路连接，浅层输入输出维度一致，可以直接相加；深层维度不一致，不能直接相加，有两种策略：（1）采用zero-padding增加维度，此时一般要先做一个downsamp，可以采用strde=2的pooling，这样不会增加参数；（2）采用新的映射（projection shortcut），一般采用1x1的卷积，这样会增加参数，也会增加计算量。短路连接除了直接使用恒等映射，当然都可以采用projection shortcut 。
Summary
ResNet的提出并不是为了解决梯度消失问题，因为当时梯度消失已有BN等方式可以缓解了。
Resnet提出的背景是，更深层的网络不应该比浅层网络差，至少也应该是一样的，因为可以恒等映射。但事实上，对于平原网络结构，更深层的网络结果可能是更糟糕的，论文里有证明了这一点。
残差的思想都是去掉相同的主体部分，从而突出微小的变化。ResNet通过残差学习解决了深层网络的退化问题。