这篇文章给我最大的感受是,虽然核心操作很简单,但是对背后的原理阐述十分清晰,实验也做的非常漂亮,值得学习。另外论文Related Work这段总结的也相当好。
论文笔记:
ELASTIC: Improving CNNs with Dynamic Scaling Policies (CVPR 2019, Oral)
Introduction
尺度变化是CV模型的一个很大的挑战,同一个数据集中,物体占据整张图片的比例可能差别很大:有的背景简单,物体占据主体;有的物体只占据整个图片很少一部分,比如草地上的高尔夫球。
目前关于尺度变化问题的解决方案比较统一,都是一些直观的人为设计的通用的、固定的规则,比如SIFT,feature pyramid。
本文作者团队任务,尺度规则应该从数据中学习到。因此,作者团队提出了ELASTIC,中文意思是松紧、松紧带。它可以有效地从数据中学习到动态缩放规则。这个缩放规则可以看作是模型中的一个非线性函数,它具有四个优点:
1. 它从数据中学习
2. 特定于实例(根据实例动态变化)
3. 不会增加额外计算量
4. 可以应用于任何网络结构
Related Work
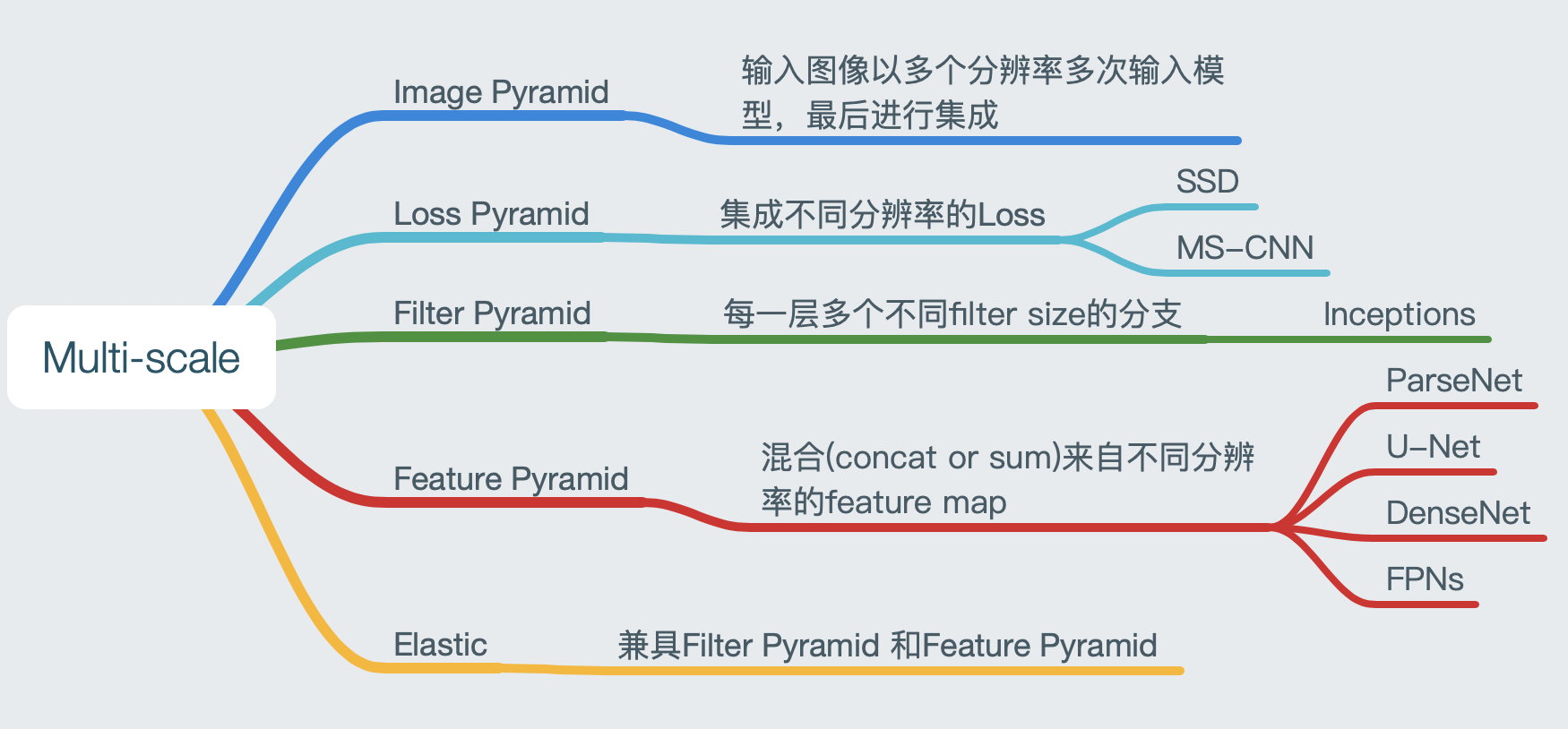

前面的结构我们大多比较熟悉,简单说一下:
- (a) Signle scale: 对应原始网络
- (b) Image pyramid: 图像金字塔是说,同一张图像用不同分辨率输入模型,对最终输出做一个集成。
- © Loss pyramid: 这种方法集成不同分辨率下的损失函数。
- (d) Feature pyramid: 最常用的方法。混合(concat,sum)来自不同分辨率的feature map。
- (e) Filter pyramid: 每一层分成多个分支,这些分支的filter size不同。典型的就是Inception系列。
Core
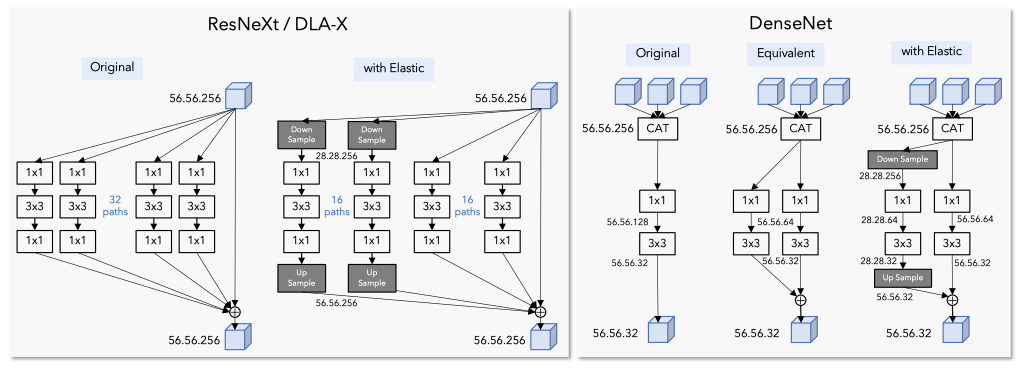
模块的核心操作,在于理解上图的f——Elastic Layer,这一层做的工作非常简单。如何集成Feature pyramid和Filter pyramid呢?parallel branches of compution + fuse information from different scales,即多分支使用不同的filter size,加上,令这些分支处理不同分辨率的信息,最后混合。
下面这幅图,用Elastic的思想,改造ResNeXt.DLA-X和DenseNet,对比图详细说明了如何在已有网络中嵌入Elastic.
为什么有效果?
这一点,论文第三章节通过理论对CNN blocks与Elastic中的Scale policy进行比较。
形式上,CNN中的一层可以表示为:
$$\mathcal{F}(x) = \sigma(\sum_{i=1}^{q}\mathcal{T}_{i}(x)) $$
其中q是之后被聚合的分支的数量,$\mathcal{T}_{i}(x)$可以是任一函数(一般是卷积、BN和激活函数的集合体),$\sigma$表示非线性。一系列的$\mathcal{F}(x)$堆叠处理一种空间分辨率形成一步,分辨率递减的多步堆叠成为一个金字塔形的缩放规则网络结构。一个网络可以被表示为:
$$\mathcal{N} = \mathcal{F}_{32} \circ \mathcal{F}_{31} \circ \mathcal{D}_{r2} \circ \mathcal{F}_{22} \circ \mathcal{F}_{21} \circ \mathcal{D}_{r1} \circ \mathcal{F}_{12} \circ \mathcal{F}_{11}$$
其中$\mathcal{D}_{r_i}$表示经过一些层后图像的分辨率缩小1倍以上。通过调整每层的输入分辨率和参数数量,可以在网络中定义一个缩放规则。找到一个最佳的缩放规则(在分辨率和参数量之间权衡)是值得尝试的。之前大部分做法(Related Work)做的还不够。
论文里提出的ELASTIC结构的单层以及整个网络公式表示为:
$$\mathcal{F}(x) = \sigma(\sum_{i=1}^{q}\mathcal{U}_{r_i}(\mathcal{T}_{i}(\mathcal{D}_{r_i}(x)))) $$
$$\mathcal{N} = \mathcal{F}_{32} \circ \mathcal{F}_{31} \circ \mathcal{F}_{22} \circ \mathcal{F}_{21} \circ \mathcal{F}_{12} \circ \mathcal{F}_{11}$$
这里的$\mathcal{D}_{r_i}(x)$和$\mathcal{U}_{r_i}(x)$分别表示下采样和上采样,改变一层中特征的空间分辨率。和传统CNN相比,主流程里面没有了下采样。
注意,这里学习到的放缩规则是可以针对特定实例的,即:对于不同的图像实例,网络可能会在每一层激活不同的分辨率分支。
对于含有复杂模式的图像,网络需要特征 高分辨率中的特征 来分类正确,那么网络靠后的层中,高分辨率分支就更可能被激活(论文第四部分验证)。
对于含有简单模式的图像,网络在低分辨率的时候就可以正确分类了,那么在网络比较靠前的层中,低分辨率分支被激活。
每一层都有不同的分辨率选择,实际上整个网络就提供了指数级的放缩可能路径。
Summary
思想: 在网络的每一层,都考虑来自不同分辨率的信息。叠加起来,Elastic在各层之间提供了指数级的缩放路径,同时保持计算复杂的与基本模型相同(甚至更少)。
核心操作:信息总是存在于高分辨率图中,每一层或者每个分支处理低分辨率或者同分辨率的图像。
收获
- 思想简单,但背后的原理讲的很透彻,多个角度解释,从和其他方法的对比,以及与传统方式相比,公式表达的变化
- 实验做的特别漂亮,多种图表结合。包括模型图、方法对比图(折线图、柱状图)、方法对比表、自定义规则、tsne图
- Related Work这段整理的特别漂亮
