About These Articles:
SVM的学习,可以查询到大量的相关文章、视频,并且在几本经典的书(西瓜书,统计学习方法等)中也有相应的解读。本文为个人总结回顾。(由于Markdown和MathJax的兼容问题,很多公式没有渲染出来,可以直接看手写推导过程。)
传送门:
简介与线性可分情况分析,最后附有详细推导过程与注解。
VC维,非线性可分情况分析,核技巧,软间隔,总结
SVM简介
Support Vector Machine(SVM),监督学习。
流行于1998年NIST的手写数字识别。其优点有:
- 是当时已有的比神经网络更有效的算法,泛化性能好,和神经网络相比不存在局部极小值,不需要长时间的收敛。
- 在许多复杂的现实应用比如文字、图片分类等任务中有成功的应用
- 在很多任务中,SVM是最好的选择
从以上我们知道,SVM是一种强大的算法,即时今天我们的神经网络已经发展出很多,有了很多优异的表现,但是这与了解SVM并不冲突,学习好SVM对于我们理解、求解一些问题依然很重要。
问题定义
训练数据:$(x_1, y_1), (x_2, y_2), … , (x_n, y_n)$, 其中,$x_i$是m维的向量,每一个向量都属于$+1, -1$中的一类。
希望寻找到一个超平面: $w·x + b = 0$,可以将训练数据分到对应的类中,正类为1,负类为-1.
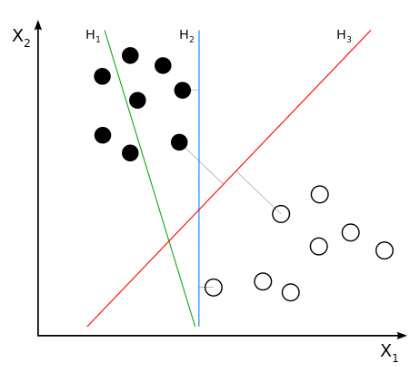
如图,虽然有无数可能的超平面,但是我们希望寻找一个泛化性能好(所谓的泛化性能好,指的是模型对没有见过的新数据依然有不错的性能,即模型表征的是一般性的特征)超平面,即上图H3的情况。
假设选定的超平面H2是靠近训练数据$x_i$的,现在对于测试数据$x^{‘}$ ,它与$x_i$同类,但是用图中选定的超平面H2却误分类类。
所以直观上,超平面的选定规则有:
- 超平面应该尽可能远离所有的样本点
- 靠近训练数据的新数据应该北正确分类
线性可分SVM
在数据线性可分的情况下,SVM 的思想是最大化超平面与最接近的样本点间的距离。在理想最优超平面处:与最近的负样本点的距离 = 与最近的正样本点的距离。最优意味着有很好的泛化性能。
Support Vectors
Support Vectors支持向量指的是距离分离超平面最近的那些样本点。即如下图所示虚线上的蓝点和绿点:
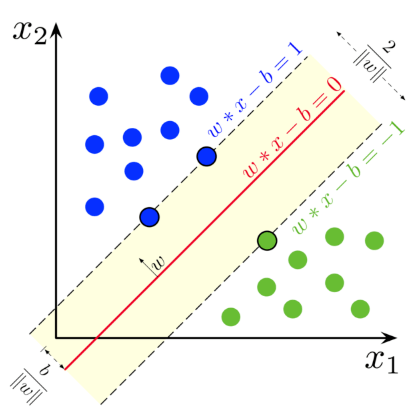
距离
假设决策边界表达式为:$w^{t}x + b = 0$ ,其中$w{\in}R^{m}, x{\in}R^{m}, b{\in}R $ 。
$\frac{w}{||w||}$ 和 决策边界垂直且长度为1。
令$\gamma_i$表示训练集中的样本点$x_i$与决策边界之间的距离。
令$x_i$为最接近决策边界的样本点集中的一个,$||w^{t}x_i + b = 1||$ ,可以 通过缩放$w,b$来满足1的条件。
此时$d = \frac{w^tx_i + b}{||w||} = \frac{1}{||w||}$ 。所以此时间隔 $m = \frac{2}{||w||}$。
寻找最优超平面
SVM通过最大化间隔$m = \frac{2}{||w||}$ 以保证:
For $y_i = +1, w^tx_i + b \geq 1$
For $y_i = -1, w^tx_i + b \leq -1$
以上的最大化问题可以等价转化为最小化$\frac{1}{2} \parallel w \parallel^2$ ,条件为$y_i(w^tx_i + b) \geq 1$ (1)。
这样转化是最优化问题转化为了一个只有线性约束并且总有单一最小值的凸二次规划问题。
最优化问题
为了求解线性可分SVM的最优化问题(1),将它作为原始最优化问题,应用拉格朗日对偶性,通过求解对偶问题得到原始问题的最优解。
这样做的优点,一是对偶问题往往更容易求解;二十自然引入核函数,进而推广到非线性分类问题。
首先构建拉格朗日函数,对每一个不等式约束引进拉格朗日乘子 $\alpha_i \geq 0, i=1,2,…,N$ (2.1),定义拉格朗日函数:
$L(w, b, \alpha)=$ $\frac{1}{2} \parallel w \parallel^2 - $$ \sum_{i=1}^{N}\alpha_i(y_i(w \cdot x_i+b) - 1 )$ (2.2),
其中 $\alpha = (\alpha_1, \alpha_2, … , \alpha_N)^T$ 为拉格朗日乘子向量。
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
$$ max_\alpha min_{w, b}L(w, b ,\alpha) $$
所以,为了得到对偶问题的解,需要先求$L(w, b, \alpha)$对$w, b$的极小,再求对$\alpha$的极大。
- 求$min_{w,b}L(w, b, \alpha)$
$\frac{\partial L}{\partial w} = 0 \Longrightarrow w = \sum_{i=1}^{n}\alpha_iy_ix_i (3)$
$\frac{\partial L}{\partial b} = 0 \Longrightarrow \sum_{i=1}^{n}\alpha_iy_i = 0 (4)$
将$(3)$代入拉格朗日函数(2)中,并利用(4),可得: $$ min_{w,b}L(w, b, \alpha) = \sum_{i=1}^{N} \alpha_i - \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) $$ 2. 求对偶问题,即$min_{w,b}L(w, b, \alpha)$ 对 $\alpha$的极大(5):
$$ max_\alpha L(\alpha) = \sum_{i=1}^{N} \alpha_i -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) $$
$$s.t. \alpha_i \geq 0 and \sum_{i=1}^{N}\alpha_iy_i=0 $$
- 原问题的解
设$\alpha^{*} = (\alpha_1^{*}, \alpha_2^{*}, … , \alpha_l^{*})^T$是对偶最优化问题(2.1,2.2)的解,则存在下标$j$,使得$\alpha_j^{*} \gt 0$,并可按下式求得原始问题的解$w^{*}, b^{*}$:
$w^{*} = \sum_{i=1}^{N}\alpha_i^{*}y_ix_i$
$b^{*} = y_j - \sum \limits_{i=1}^{N} \alpha_i^{*} y_i ( x_i \cdot x_j )$
最终得到我们的决策函数:
$f(x)=sign(w^{*}x+b^{*})$
小结:线性可分SVM学习算法
输入: 线性可分训练集$T = {(x_1, y_1), (x_2, y_2), …, (x_N, y_N)}$,其中$x_i\in R^n, y_i \in {+1, -1}, i=1, 2,…,N$
输出: 分离超平面和分类决策函数
(1) 构造并求解约束最优化问题
$\underset{\alpha}{\text{min}} \frac{1}{2} \sum\limits_{i,j}^n \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) - \sum\limits_{i=1}^{N} \alpha_i$
$min_\alpha \frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^{N}\alpha_i$
$s.t. \sum_{i=1}^{N}\alpha_iy_i = 0$
$\alpha_i \ge 0, i = 1, 2,…,N$
(2) 计算
$w^{*} = \sum_{i=1}^{N}\alpha_i^{*}y_ix_i$
并选择$\alpha^{*}$的一个正分量$\alpha_j^{*} \gt 0$,计算
$b^{*}=y_j- \sum_{i=1}^{N} \alpha_i^{*} y_i(x_i \cdot x_j)$
(3)求得分离超平面
$w^{*} \cdot x + b^{*} = 0$
分离决策函数:
$f(x)=$ $sign(w^{*}x+b^{*})$
附: 手写推导过程
结合本图:


