初学CNN的时候,比较疑惑输入的维度是(BatchSize, Channels, Height, Width)的feature map经过size是k的卷积核后变成了输出是什么?以及它是怎么实现的?
本文主要讲解并探究卷积实现。
首先简单聊一下卷积操作,介绍Pytorch中卷积的API;
接着我们自己用python实现简单卷积,并与API调用结果进行对比;
之后我们进一步去了解Pytorch中卷积的实现源码。
「更新」,element-width卷积的实现。
Brief Introduction
卷积是当下流行的计算机视觉模型架构的最基础的构造单元,从分类模型(如ResNet)到对抗生成网络(如DC-GAN),再到目标检测架构(以Mask R-CNN为代表)以及其他的大大小小的模型,卷积操作可以完成大部分计算繁琐的工作。
对与卷积的理解与解释有很多已有的优秀博文,附上传送门,本文不多追述。
- Wiki
- 什么是卷积
- CS231n
卷积运算表面上看就是,在滤波器和输入数据的局部区域间做点积,下面的GIF用滑窗的方式表明了其是如何操作的1 。
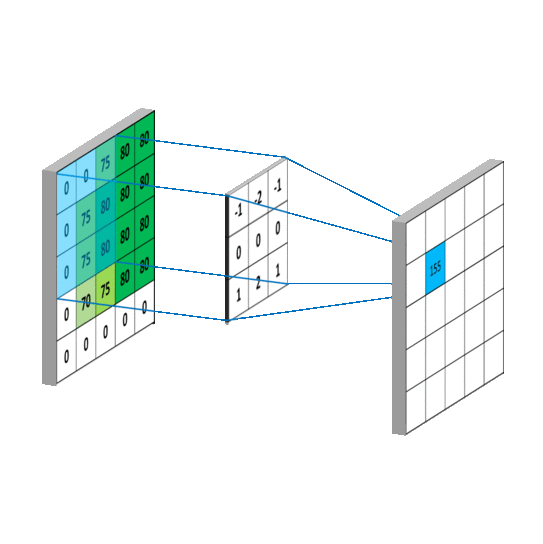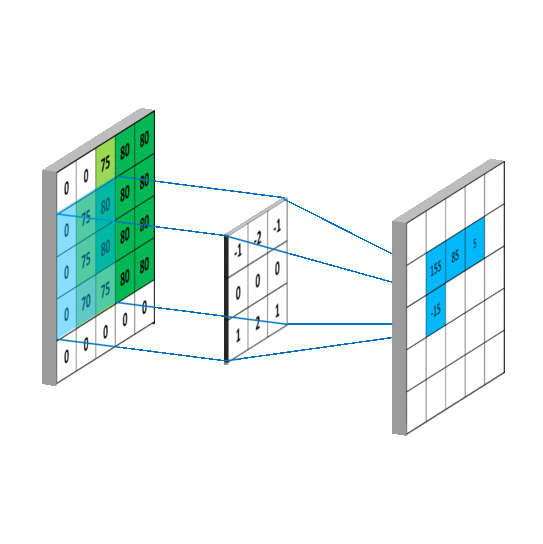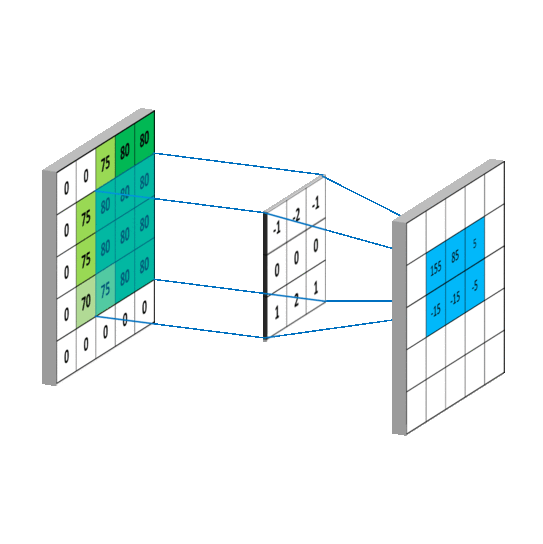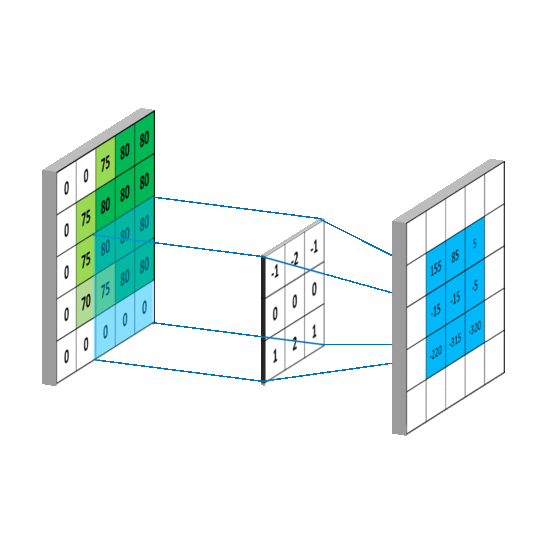
Params
CNN中当卷积核size确定之后,控制输出feature_maps的shape的有三个超参数,分别是depth,stide,zero-padding:
1. 输出feature_maps的depth: 它对应我们想要使用的卷积核的数量,每个卷积核都在输入中学习寻找不同的特征。例如,如果第一卷积层将原始图像作为输入,则沿着深度维度的不同神经元可以在存在各种定向边缘或颜色、斑点的情况下激活。
2. 滑动卷积核的步幅stride: 当stride=1时,每次移动卷积核一个像素;当stride=2时,一次跳跃2个像素(实践中很少用stride>=3,会丢失信息),这会导致输出的size变小。
3. zero-padding:有时在边界周围用零填充会很方便,它允许我们控制输出feature_map的空间大小,最常见的是,我们需要保持输出和输入的大小一样。就像上面第二张图中的那样,在输入的feature_map四周补上0。通常,当步幅stride=1时,将零填充设置为P = (F-1)/2,例如(F,P)=(3,1),(5,2),(7,3)。
Pytorch API
这里以torch.nn.Conv2d为例。
class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)当输入是$(N, C_{in}, H, W)$时,输出$(N, C_{out}, H_{out}, W_{out})$可以用以下公式计算得到。
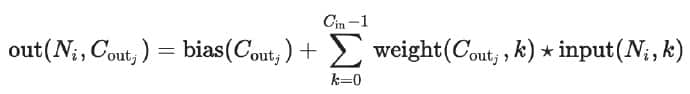
其中 ★ 表示相关卷积操作,$N$表示 batch size, $C$ 表示channels(通道)数量,即feature_map 的数量,$H, W$表示feature_map的像素高度和宽度。
在理解了上小节的Params后,我们就不难理解API中参数的含义了。这篇文章将API解读得很详细(尤其是对group参数的解释)。
值得一提的是API中kernel_size,stride,padding参数既可以是一个单一的整数(表示横行和纵向移动相同的单位长度),也可以是由两个整数构成的tuple对象。如果是两个整数,那么运算的时候,横向步长为第一个参数,第二个参数是纵向步长。
现在回到文章最开头提的问题,输入的形状是$(N, C_{in}, H, W)$,输出的形状是$(N, C_{out}, H_{out}, W_{out})$,它们之间的关系可以由kernel_size,stride,padding表达。假设我们不考虑PyTorch文档中的dilation参数,我们可以得到如下的关系式:
$$ H_{out} = [\frac{H_{in} + 2 \times padding[0] - (\text{kernel_size}[0] - 1) - 1}{stride[0]} + 1] $$
$$ W_{out} = [\frac{W_{in} + 2 \times padding[1] - (\text{kernel_size}[1] - 1) - 1}{stride[1]} + 1] $$
看到这个公式,我们就不难理解上面的如何保持$H_{out},H_{in}$尺寸相同了。一般情况下,我们设置stride=1,那么就有:
$$ 2 \times padding[0] = \text{kernel_size}[0] - 1 $$
所以,以后就可以根据这个公式灵活得到与kernel_size对应的padding了。常用的组合有$(k,p) = (3, 1), (5, 2), (7, 3)$。
Numpy Implementation
本小结,我们尝试使用Numpy来实现卷积运算,实现上面图中的运算,并将结果和调用PyTorch的API的结果进行对比验证。
Simple Convolution
首先,实现一个最基本的卷积过程,这个卷积运算是单通道输入、单通道输出的,用作卷积的最基础的运算模块。为了方便起见,这里我们设定stride=1。
import numpy as np
def baseConv(feature_map, kernel):
'''
Args:
feature_map: [H, W]
kernel: [k, k]
Returns:
out: [H, W]
'''
h, w = feature_map.shape
k, _ = kernel.shape
# padding
p = int(k / 2)
# add zeors padding
feature_map_padding = np.zeros([h + p * 2, w + p * 2])
feature_map_padding[p:h + p, p:w + p] = feature_map
result = np.zeros([h, w])
for i in range(h):
for j in range(w):
# region of interest
roi = feature_map_padding[i:i + k, j:j + k]
result[i][j] = np.sum(roi * kernel)
return resultConv2d
以上只是最简单版本的单通道输入、单通道输出的卷积过程。然而,我们在实际运算的过程中用到的都是多通道输入、多通道输入的卷积。在上述模块的基础上,我们可以很容易地实现多通道输入多通道输入的卷积运算过程。只需要使用两个for循环,遍历每一个通道的输入和每一个通道的输出即可。如下所示。
def conv2d(input, weights):
'''
Args:
input: [C_in, H, W]
weights: [C_out, K, K]
Returns:
out: [C_out, H, W]
'''
in_channel, h, w = input.shape
out_channel, *_ = weights.shape
output = np.zeros( [out_channel, h, w] )
for i in range(out_channel):
weight = weights[i]
for j in range(in_channel):
feature_map = input[j]
kernel = weight[j]
output[i] += baseConv(feature_map, kernel)
return outputTest
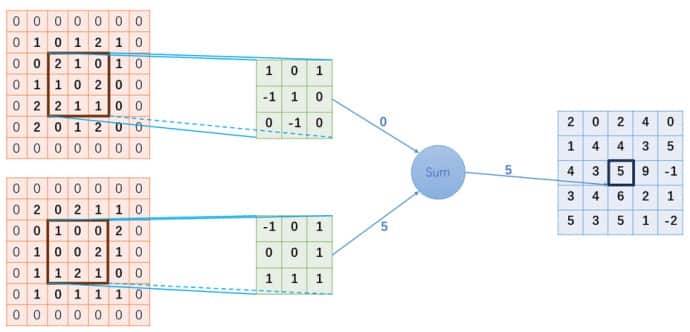
写好函数后,我们使用上面图片里的数据来验证一下程序运算结果的正确性。
input_data=[ [[1,0,1,2,1],
[0,2,1,0,1],
[1,1,0,2,0],
[2,2,1,1,0],
[2,0,1,2,0]],
[[2,0,2,1,1],
[0,1,0,0,2],
[1,0,0,2,1],
[1,1,2,1,0],
[1,0,1,1,1]],]
weights_data=[[ [[ 1, 0, 1],
[-1, 1, 0],
[ 0,-1, 0]],
[[-1, 0, 1],
[ 0, 0, 1],
[ 1, 1, 1]]
]]
# change list into numpy array
input = np.array(input_data)
weights = np.array(weights_data)
# show the result
print(conv2d(input, weights))
#[[[ 2. 0. 2. 4. 0.]
# [ 1. 4. 4. 3. 5.]
# [ 4. 3. 5. 9. -1.]
# [ 3. 4. 6. 2. 1.]
# [ 5. 3. 5. 1. -2.]]]下面我们再用Pytorch里面的torch.nn.functional.conv2d来验证一下。
import torch.nn.functional as F
input = torch.tensor(input_data).unsqueeze(0).float()
weights = torch.tensor(weights_data).float()
result = F.conv2d(input, weights, padding=1)
# tensor([[[[ 2., 0., 2., 4., 0.],
# [ 1., 4., 4., 3., 5.],
# [ 4., 3., 5., 9., -1.],
# [ 3., 4., 6., 2., 1.],
# [ 5., 3., 5., 1., -2.]]]])验证完毕。
PyTorch Source Code
现在我们来追本溯源,看看PyTorch中是如何实现conv操作的。
当我们在PyCharm中追也只能看到nn.Conv2d调用了nn.functional.conv2d,再往下就没有了。
Stackoverflow的这个回答提醒了我。

我们如果是依赖于GPU,那么要去cudnn里找,但是cudnn是闭源的,看不到底层的实现。但是对于CPU版本,我们知道它的底层还是用C,C++来实现的,所以从这方面着手,找了Github里pytorch.torch.csrc,依然没有哦。
所幸的是,我找到了这个aten。src里的说明文件表明这是PyTorch的底层tensor库。我们要找CPU版本的,所以直接在TH=TorcH里寻找,终于找到了这份实现。我们截取部分代码分析一下:
/*
2D Input, 2D kernel : convolve given image with the given kernel.
*/
void THTensor_(validXCorr2Dptr)(scalar_t *r_,
scalar_t alpha,
scalar_t *t_, int64_t ir, int64_t ic,
scalar_t *k_, int64_t kr, int64_t kc,
int64_t sr, int64_t sc)
{
int64_t or_ = (ir - kr) / sr + 1;
int64_t oc = (ic - kc) / sc + 1;
int64_t xx, yy, kx, ky;
if ((sc != 1) || (oc < 4)) {
/* regular convolution */
for(yy = 0; yy < or_; yy++) {
for(xx = 0; xx < oc; xx++) {
/* Dot product in two dimensions... (between input image and the mask) */
scalar_t *pi_ = t_ + yy*sr*ic + xx*sc;
scalar_t *pw_ = k_;
scalar_t sum = 0;
for(ky = 0; ky < kr; ky++) {
for(kx = 0; kx < kc; kx++) {
sum += pi_[kx]*pw_[kx];
}
pi_ += ic; /* next input line */
pw_ += kc; /* next mask line */
}
/* Update output */
*r_++ += alpha*sum;
}
}
} else {
/* SSE-based convolution */
...
}
}
首先它的数据类型,都是在C++数据类型后面加了_t,应该是表示这个Tensor类型基本类型。
接着是他的参数,ir, ic表示输入的row和col,同理kr, kc,sr, sc分别表示kernel和stride的像素长度。
函数体前两行先定义了输出的row和col;接下来对sc和oc的判断是为了使用SSE-based convolution,我们选择忽略,直接看if的代码块内容,发现外层两个循环和我们上面实现的baseConv里的循环h,w一样,为了计算输出的每个像素点的最终值;而内层的两个循环则是做卷积操作得到新的像素值,我们则是利用了numpy的计算便利性;*r_++ += alpha*sum左边*r表示的是返回数据的引用,通过自增改变对应地址的元素,右边的alpha应该是卷积的权重。
Element Width Convolution
【2019年3月12日更新】
上面的讨论中一直忽略了groups这个参数,这个参数的功能还是相当强大的。
目前我们了解到的卷积都是cross-related的,就是说下一层的每个神经元都有前一层所有神经元的贡献,贡献多少就是需要学习的权值。
现在有两种情况:
- 1 假设有些神经元无关,下一层不想要它贡献,即使可以设置其权值为0,但是无法单个冻结。
- 2 假设我们自定义了一个操作,它实现的是对上一层([B,C,H,W])每个feature map(即C个),都分别做操作,做完之后再传到下一层。当然这个操作是不影响反向传播的。
类似这个时候,我们就可以利用groups参数。它控制着输入和输出之前的连接,隐含条件是输入和输出的通道数量要能被groups整除。
- 当groups=1时,所有的输入都经过卷积到输出。
- 当groups=2时,该操作变得等同于并排具有两个卷积层,每个卷积输入通道的一半,并且产生输出通道的一半,并且随后连接。
- 当groups=in_channels时,每个输入只和它对应的一组卷积(共 $\frac{C_{out}}{C_{in}}$ 个)进行卷积。
Summary
至此,我们发现我们的实现和PyTorch的底层实现其实是相同的。
感谢崔哥提供的支持。
-
多种卷积动图请见--> Github
