8-puzzles algorithm ·

AIMA: 8-puzzles

题目描述

8-puzzle problem
Given any randomly generated start state and a goal state shown below, implement the IDS, greedy search and A* search algorithms, respectively, to find a sequence of actions that will transform the state from the start state to the goal state.

topics: DFS, IDS, A*, Greedy, Informed Search ¹

要求

1) When implementing the A* search algorithm, you need to use at least two different
heuristic functions
2) Compare the running time of these different searching algorithms, and do some
analyses on your obtained results. Note that the reported running time should be
averaged on many randomly generate different start states.

问题解析

是否有解

首先对于八数码问题，存在有解和无解的情况，为了使得我们后续的程序能正常测试，我们需要对给定的随机初始状态进行检测，从而得到一定有解的随机初始状态。
根据维基百科，如果给定初始状态的逆序和为偶数，那么问题有解，否则无解。

生成有解的随机初始状态有两种做法。一是生成随机的状态，检测是否有解，无解则继续生成，直到生成有解的状态并返回。二是逆序推导，从目标状态出发，随机选择方向走若干步得到随机状态。

这里我们为了方便，将空白格用数字0表示。

两种做法的代码如下：

# Solution 1: genRandomState->check->genRandomState....
def genRandomState():
    puzzle = [x for x in range(9)]
    random.shuffle(puzzle)
    puzzle = np.asarray(puzzle).reshape((3,3))
    return puzzle
# getInvCount
def getInvCount(state):
    state = state.flatten()
    int_count = 0
    for i in range(8):
        for j in range(i+1, 9):
            if state[j] and state[i] and state[i] > state[j]:
                int_count += 1
    return int_count
# judge
def isSolvable(state):
    invCount = getInvCount(state)
    return invCount % 2 == 0:

def genSolvableRandomState():
    puzzle = genRandomState()
    if isSolvable(puzzle):
        return puzzle
    else:
        return genSolvableRandomState()

# Solution 2: targetState->randomWalk->randomState  
def shuffle(self, numAct):
    for i in range(numAct):
        self.move(self.directions[random.randint(0, 3)])

def move(self, direction):
    if direction == 'U':
        self.up()
    if direction == 'D':
        self.down()
    if direction == 'L':
        self.left()
    if direction == 'R':
        self.right()

思考：
第二种做法里，我们需要对状态做一些变化，从当前状态到下一个状态，需要判断可以走的方向，并更新0点的位置，都是一些可以重复并高度聚合的方法，因此可以将这些操作都封装到Puzzle类中。

IDS

IDS算法的伪代码如下：

IDS(Iterative deepening search)的核心在于，使用迭代深度限制深度搜索，使得每次只搜索到指定的深度。因此也需要对DFS有较深的理解。
这样做虽然会使得高层的节点被反复访问多次，但是可以推导出，最底层的节点数是最多的，将问题简化为二叉树，那么最底层有总体一半的节点，同时我们需要前序节点的信息去访问后续节点，因此在深度较深的时候，前面反复访问的时间可以不用去管。
Depth-Limited-Search基于DFS，DFS的伪代码如下：

思考：这里我们需要维护的信息是深度信息，而且由于当前状态可能的子节点最多有四个，所以子节点的信息最好和父节点绑定，所以在设计Puzzle类的时候，我们可以绑定父节点parent，计算与判断当前节点的深度也相对方便。
在IDS中，我们更多的需要对节点进行操作，而不是直接对Puzzle操作，所以可以尝试构建Node类，简化代码逻辑。

IDS实现代码如下：

def IDS(self):
    depth = 0
    result = None
    while result == None:
        result = self.depthLimited(depth)
        depth += 1
    return result

def depthLimited(self, depth):
    stack = LifoQueue()
    stack.put(self.start)
    while True:
        if stack.empty():
            return None
        top = stack.get()
        if top.isGoal():
            return top
        elif top.depth is not depth:
            for neighbor in top.neighbors():
                stack.put(neighbor)

Uninformed v.s. Informed search

Uninformed Search，不知情搜索，无先验知识的搜索，通俗一点理解就是摸着石头过河，把所有可能的路都走一遍。个人理解，不同之处就在于走的顺序是全随机，还是半随机，对于DFS和BFS，可以归类为全随机，而IDS可以算半随机。
Uninformed Search，先验搜索，启发式搜索，像是有了一把自己定义的尺子，可以衡量某一状态到目标状态的距离，通过这个先验知识去确定下一个最接近目标状态的中间状态。

Greedy

对中间状态的选择取决于其到目标状态的“距离”，这个距离可以有不同的衡量标准。贪心算法基于“距离”，通过维护一个优先队列，每次选择距离目标状态最近的中间状态去扩展。为了避免陷入死循环，维护visited数组。
贪心算法的实现如下：

def greedy(self, heuristic_mode):
    cur_node = self.start
    nodes = PriorityQueue()
    nodes.put((cur_node.cost(heuristic_mode), cur_node))
    visited = []
    while True:
        if nodes.empty():
            return None
        cur_node = nodes.get()[1]
        if cur_node.isGoal():
            return cur_node
        elif cur_node.state.puzzle not in visited:
            visited.append(cur_node.state.puzzle)
            for neighbor in cur_node.neighbors():
                nodes.put((neighbor.cost(heuristic_mode), neighbor))

A*

启发式函数h(n)告诉A*从任何结点n到目标结点的最小代价评估值。因此选择一个好的启发式函数很重要。
A* 计算f(n) = g(n) + h(n)。为了将两个值相加，这两个值必须使用相同的单位去度量。如果度量g(n)的单位是小时，衡量h(n)的单位是米，则A*将认为g或h太大或太小，因此，要么无法得到好的路径，要么A*的运行速度会更慢。
A*算法的伪代码如下：

A*算法实现如下：

def aStar(self, heuristic_mode):
    cur_node = self.start
    nodes = PriorityQueue()
    nodes.put((cur_node.cost(heuristic_mode), cur_node))
    visited = []
    while True:
        if nodes.empty():
            return None
        cur_node = nodes.get()[1]
        if cur_node.isGoal():
            return cur_node
        elif cur_node.state.puzzle not in visited:
            visited.append(cur_node.state.puzzle)
            for neighbor in cur_node.neighbors():
                nodes.put((neighbor.cost(heuristic_mode) + neighbor.depth, neighbor))

启发式函数

针对八数码问题，考虑两个相对间的的启发式函数：
1. wrongPlace，摆放位置错位的数字个数。
2. distance_manhattan，曼哈顿距离，计算元素当前位置到目标位置的曼哈顿距离之和。

两个启发式函数的代码如下：

def cost(self, heuristic_mode):
    return self.placeWrong() if heuristic_mode == 0 else self.distance_manhattan()

def placeWrong(self):
    errors = 0
    count = 1
    all = self.state.order ** 2
    for i in range(self.state.order):
        for j in range(self.state.order):
            if self.state.puzzle[i][j] != count % all:
                errors += 1
            count += 1
    return errors

def distance_manhattan(self):
    res = 0
    for i in range(self.state.order):
        for j in range(self.state.order):
            index = self.state.puzzle[i][j] - 1
            dis = 0 if index == -1 else abs(i - int(index/self.state.order)) + abs(j - int(index % self.state.order))
            res += dis
    return res

代码

Puzzle, Node

上文的两段思考提到，首先需要将Puzzle的生成、移动、深度等方法或属性集成；接着，我们的算法操作的都是状态节点，而不是状态本身，为了方便对Puzzle进行堆栈、队列操作，同时分离二者有助于我们后续添加算法，因此再构建Node类，并将启发式函数归为本类。

Solution

在solution.py中，集成了问题求解的几个算法。

Others

在misc.py中，设计了两个函数计算随机生成状态的逆序和，以及判断是否可解。
最终测试结果在AIMA_HW1_Test.ipynb文件中。

结果分析

生成30个随机初始状态。

order = 3
steps = 30
puzzles = []
for i in range(30):
    t = puzzle.Puzzle(order)
    t.shuffle(steps)
    puzzles.append(t)

生成的随机初始状态如下：

1 0 2 2 3 6 1 2 3 1 3 0 7 6 3 1 4 0 4 8 5 5 2 6 5 4 8 7 5 8 7 6 0 4 7 8

1 8 2 2 5 3 1 3 5 1 3 6 5 4 3 4 1 0 4 2 0 4 0 8 0 7 6 7 8 6 7 8 6 7 2 5

0 2 3 1 5 2 1 5 2 4 1 2 1 5 6 0 4 3 3 7 6 5 3 0 4 7 8 7 8 6 4 0 8 7 8 6

2 4 3 1 0 5 1 2 3 1 2 3 0 7 5 4 3 2 7 4 6 4 0 6 8 1 6 7 8 6 0 5 8 7 5 8

…

执行不同搜索算法，并记录平均执行时间：

# 0: Greedy with wrongplace cost
# 1: Greedy with manhattan cost
# 2: A* with wrongplace cost
# 3: A* with manhattan cost
# 4: IDS
def eval(puzzles, algos):
    timeuse = []
    for i in algos:
        start = time.time()
        if i == 4:
            print("-------------------IDS------------------------")
            for t in puzzles:
#                 t.toString()
                s = solution.Solution(t)
                print("Routes:", s.IDS())
        elif i == 0:
            print("----------Greedy heuristic wrongPlace----------------")
            for t in puzzles:
#                 t.toString()
                s = solution.Solution(t)
                print("Routes:", s.greedy(0))
        elif i == 1:
            print("----------Greedy heuristic manhattan----------------")
            for t in puzzles:
#                 t.toString()
                s = solution.Solution(t)
                print("Routes:", s.greedy(1))
        elif i == 2:
            print("-------------A* heuristic wrongPlace----------------")
            for t in puzzles:
#                 t.toString()
                s = solution.Solution(t)
                print("Routes:", s.aStar(0))
        elif i == 3:
            print("-------------A* heuristic manhattan-----------------")
            for t in puzzles:
#                 t.toString()
                s = solution.Solution(t)
                print("Routes:", s.aStar(1))

        print("--------------------Time------------------------------")
        during = time.time() - start
        timeuse.append(during)
        print(during/len(puzzles))
        print("----------------------------------------------------------")
    return timeuse

timeuse = eval(puzzles, [4, 0, 1, 2, 3])
print(timeuse)

执行结果

IDS执行结果

Greedy, wrongPlace执行结果

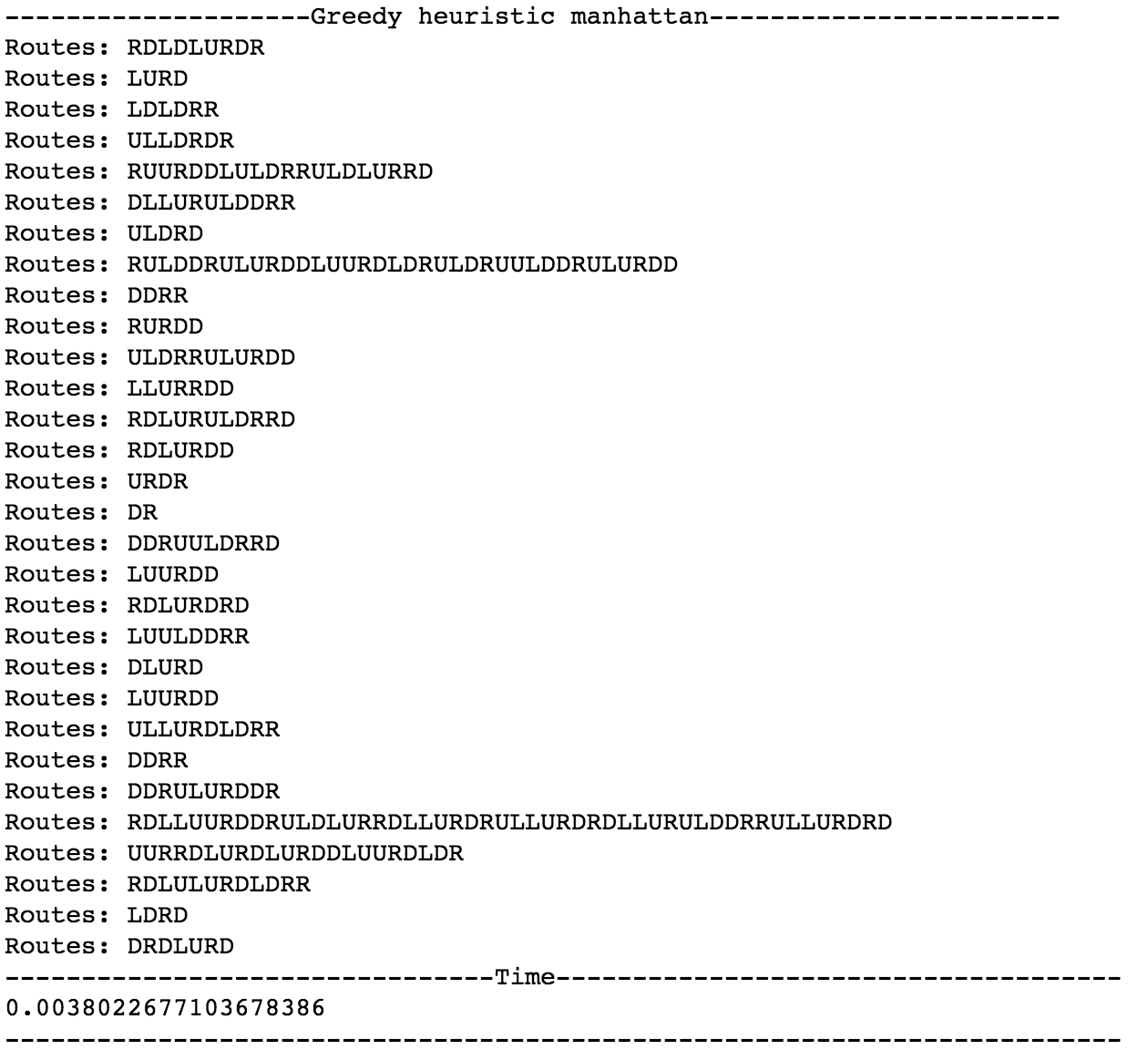
Greedy, manhattan执行结果

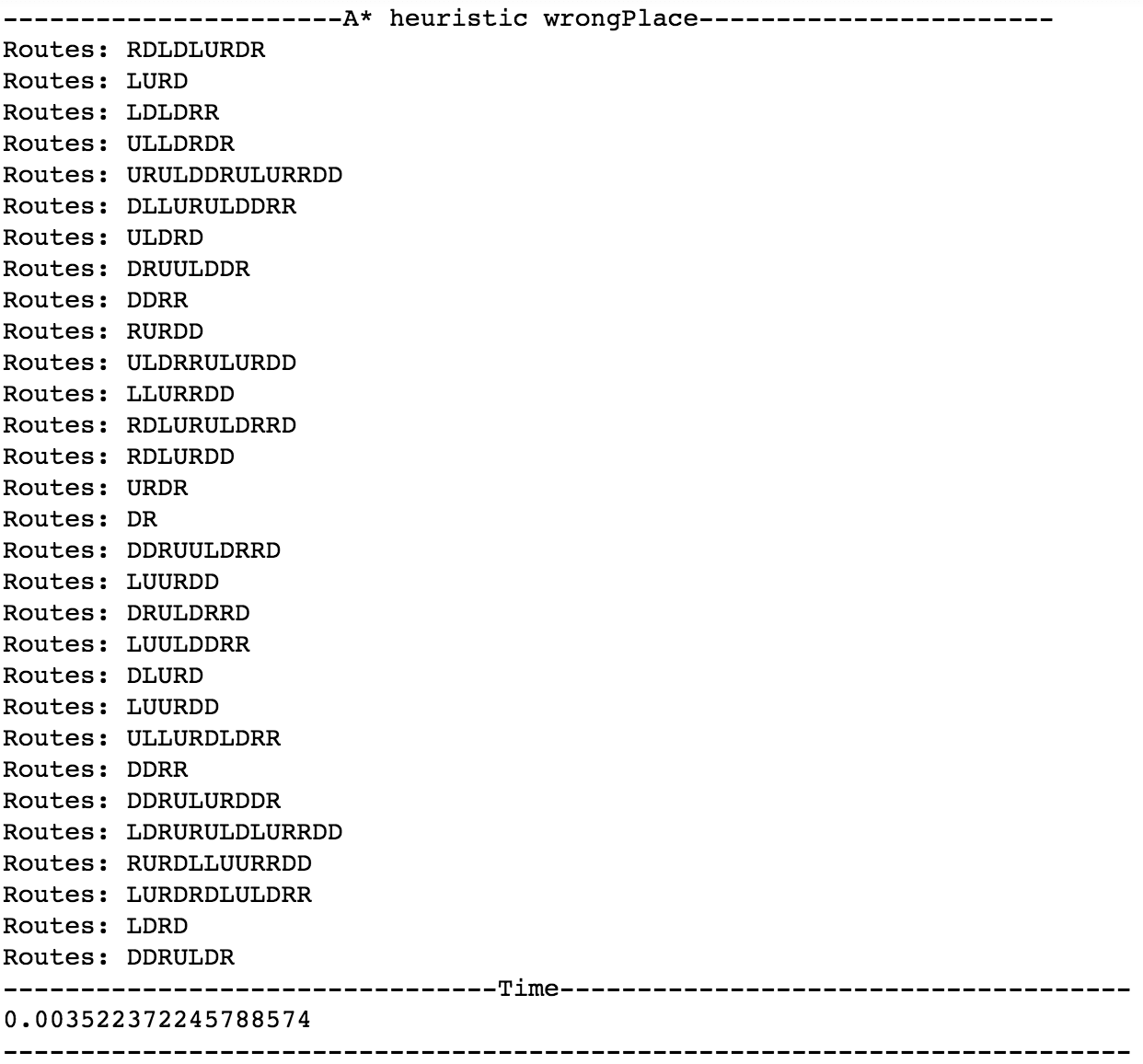
AStar, wrongPlace执行结果

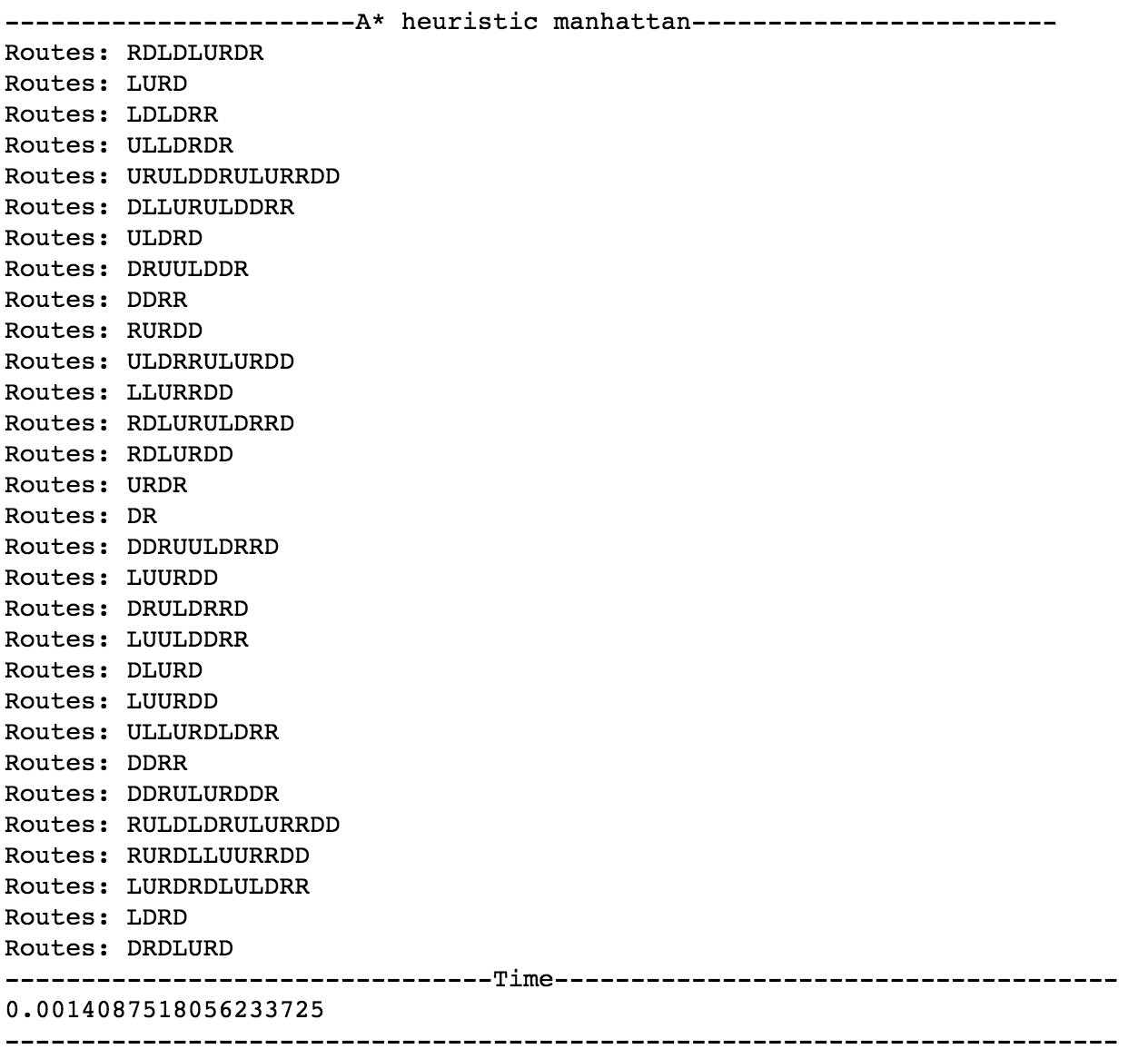
AStar, manhattan执行结果

结果分析

不同方法比较

IDS, Greedy与A*算法表现出了截然不同的性能。IDS的执行情况非常不理想，其余二者的算法表现都令人相当满意。经过多次的生成以及执行，发现Greedy与A*相对稳定，基本上可以保持这个平均用时得到解路径；但是IDS经常性出现执行时间明显过久。

不同启发式函数比较

本次实验用了两个启发式函数，分别是 wrongPlace（摆放位置错位的数字个数）、distance_manhattan（曼哈顿距离，计算元素当前位置到目标位置的曼哈顿距离之和）。分析可知，曼哈顿距离的度量包含了错误摆放度量的结果。因此，使用曼哈顿距离的算法表现应该相对较好。实验也证实了这一点，在Greedy算法中，distance_manhattan比wrongPlace执行快约7倍；在A*算法中，distance_manhattan比wrongPlace执行快约3倍。

总结

经过本次实验，我对经典的搜索算法有了深刻的认识，在编写Solution代码的时候，通过抽取公用代码，极大简化了代码并降低了最终的代码量。通过对比两个启发式函数，理解了一个“好的”启发式函数对问题求解的重要性。

source code->github

Source Code. If you like it, please give a star!